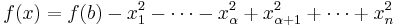Gradient-like vector field

In differential topology, a mathematical discipline, and more specifically in Morse theory, a gradient-like vector field is a generalization of gradient vector field.

The primary motivation is as a technical tool in the construction of Morse functions, to show that one can construct a function whose critical points are at distinct levels. One first constructs a Morse function, then uses gradient-like vector fields to move around the critical points, yielding a different Morse function.

Definition

Given a Morse function f on a manifold M, a gradient-like vector field X for the function f is, informally:

away from critical points, X points "in the same direction as" the gradient of f, and
near a critical point (in the neighborhood of a critical point), it equals the gradient of f, when f is written in standard form given in the Morse lemmas.

Formally:^[1]

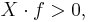
away from critical points, $X \cdot f > 0,$
around every critical point there is a neighborhood on which f is given as in the Morse lemmas:

$f(x) = f(b) - x_1^2 - \cdots - x_{\alpha}^2 %2B x_{\alpha %2B1}^2 %2B \cdots %2B x_n^2$

and on which X equals the gradient of f.

Dynamical system

The associated dynamical system of a gradient-like vector field, a gradient-like dynamical system, is a special case of a Morse–Smale system.

References

^ p. 63

An introduction to Morse theory, Yukio Matsumoto, 2002, Section 2.3: Gradient-like vector fields, p. 56–69
Gradient-Like Vector Fields Exist, September 25, 2009